我们知道python应用在各行各业中,在一些行业的建模中我们会涉及到一些比较专业的物理模型。比如多径效应,python可以和matlab一样很好地实现这些物理模型的建模,今天我们就来了解一下python实现仿真双径效应的方法。
多径效应
多径效应(multipath effect):指电磁波经不同路径传播后,各分量场到达接收端时间不同,按各自相位相互叠加而造成干扰,使得原来的信号失真,或者产生错误。比如电磁波沿不同的两条路径传播,而两条路径的长度正好相差半个波长,那么两路信号到达终点时正好相互抵消了(波峰与波谷重合)。通常采用一些近似方法来描述信号的传播特性,其中最常见的一种近似方法是射线跟踪计算。射线跟踪模型将波前近似为简单粒子,进而确定出反射和折射对波前的影响。最简单的射线跟踪模型是双径模型,指发射机和接收机之间只存在一条直射路径和一条反射路径的情况。双径模型中的反射信号一般为地面反射,对于高速公路以及乡村道路和水面上的信号传播来说,双径模型是一种很好的近似,能够准确地反映信号的传播特性。
双径模型
双径模型用在单一的地面反射波在多径效应中起主导作用的情形,如下图所示是双径模型的示意图。接收信号由两部分组成:经自由空间达到接收端的直射分量和经过地面反射到达接收端的反射分量。
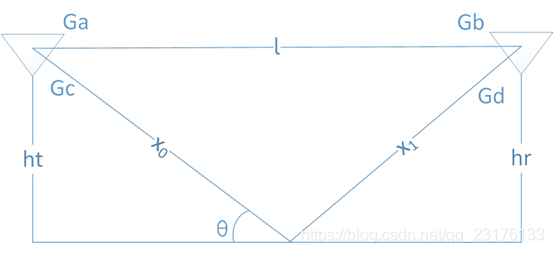
双径模型中的接收信号为:
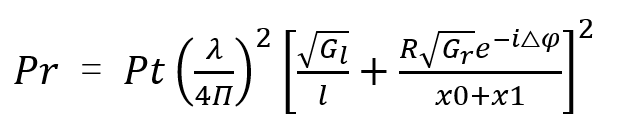
Pt为发射功率,Gt为自射天线增益乘积GaGb,Gr为反射路径天线增益乘积GcGd,l为直射的路径,x0+x1为反射的路径,△φ为反射路径和直射路径的相位差,△φ=2Π(x0+ x1-l)/λ,反射系数R≈0.9。
模型分析
假设通信频率为2000MHz,基站高度1m,手持终端高度为1m,l=18m,此时θ=actan(1/18x2) =6.353°,x0=x1=1/sin(6.353°)=9.0373m,△φ=360°x(x0 +x1-l)/λ=179°。入射波和反射波相差接近180°相位,相互抵消,这时候接收功率就出现了极小值。
按照上述的设定值,绘制4m-150m的接收功率图如下:
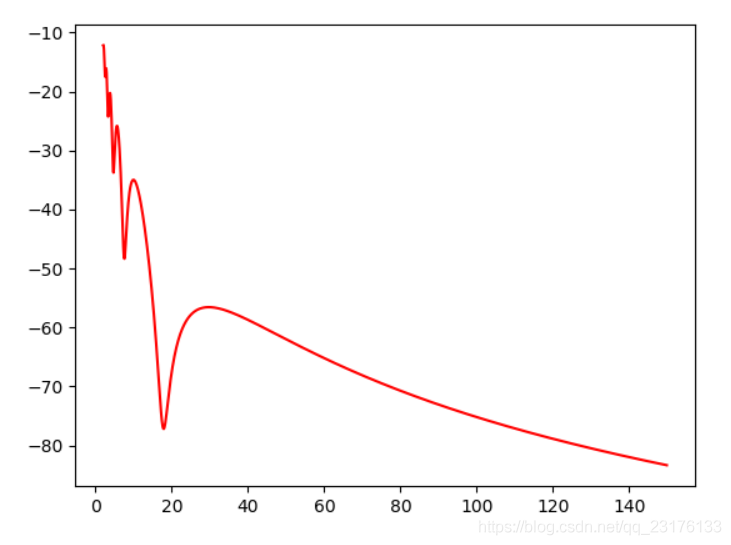
双径模型仿真程序
import numpy as np
import matplotlib.pyplot as plt
def Radiation( theta, kt=0.2):
theta = theta+np.pi/2
pi = np.pi
gmax_t = (np.cos(2 * pi * kt * np.cos(pi / 2)) - np.cos(2 * pi * kt)) / np.sin(pi / 2)
gain = (np.cos(2 * pi * kt * np.cos(theta)) - np.cos(2 * pi * kt)) / np.sin(theta) / gmax_t
return gain**2
def multipath_effect():
h_j = 1
h_c = 1
f = 2
lamda = 0.3 / f
x = []
y = []
for i in range(20, 1500):
l = i / 10
x.append(l)
l_c = h_c / (h_j + h_c) * l
l_j = h_j / (h_j + h_c) * l
lx = (h_c ** 2 + l_c ** 2) ** 0.5 + (h_j ** 2 + l_j ** 2) ** 0.5
ly = (l ** 2 + (h_c - h_j) ** 2) ** 0.5
l_d = lx - ly
phase = l_d / lamda * 2 * np.pi
theta_z = np.arctan(abs(h_j - h_c) / l)
theta_f = np.arctan(h_j / l_j)
tmp = Radiation(theta_z) * Radiation(theta_z) / ly ** 2 + Radiation(theta_f) * Radiation(theta_f) / lx ** 2 * np.sin(phase)
y.append(20 * np.log10(tmp))
plt.plot(x, y, 'r-')
plt.show()
multipath_effect()
到此这篇Python实现仿真双径效应的方法就介绍到这了,希望能对各位小伙伴有帮助,也希望大家以后多多支持W3Cschool!

 免费AI编程助手
免费AI编程助手



